The next mission to Jupiter will be revolutionary - a nuclear powered monster, a hundred times more capable than Galileo. Never before in space exploration has such a dramatic improvement in capability been encountered.

An artist's concept of Jupiter Icy Moons Orbiter. Credit: NASA/JPL

Scientists had expected to fly a small (perhaps 300 kg) Europa orbiter late in this decade, in order to confirm the presence of an ocean and study the thickness, structure and composition of the ice overlying it. However, such a mission posed extreme technical challenges for two main reasons. First, it takes an enormous amount of propulsive ability (in other words rocket fuel!) to reach Jupiter, then descend into its gravity well and enter orbit around Europa. The second challenge is the intense radiation around Jupiter's inner two satellites.

Although a Europa Mission had been firmly in NASA's plans, these technical obstacles proved too serious, and the miss ion's cost grew unacceptably, forcing it to be shelved.

By the throat
Against this backdrop, scientists were dumbfounded to learn of NASA's new plan, which grips the problem of propulsive ability by the throat. NASA will spend $2 billion over the next few years to develop a fleet of nuclear-powered spacecraft. No one knows what the program will eventually cost - certainly several billions, perhaps with some cash from other US government agencies. But NASA and the US administration is solidly behind the project - dubbed Prometheus after the thief of fire from the gods, who gave it to man. Already three contracts, each worth $6 million, have been awarded to industrial contractors for early studies.

The first of these spacecraft is called JIMO - the Jupiter Icy Moons Orbiter, which will use ion drives powered by a l a rge nuclear reactor to spiral away from Earth and orbit, for several months each, the Jovian satellites Callisto, Ganymede and Europa.

Ion vs Chemical
Chemical rockets burn chemicals to make them hot, and then expand the exhaust gases through a nozzle to shoot them backwards at around 3 km/s. By Newton's 'equal but opposite reaction' law, this propels the spacecraft forwards. Ion drives accelerate an ionized gas through an electric field and no combustion process limits its exhaust velocity. Usually inert xenon gas (used in flashbulbs) is used and accelerated to 30 km/s giving ten or more times as much push for the same amount of chemical propellant.

While a Europa Orbiter can, in principle, be achieved - just - with chemical rockets, a grand tour of the Jovian system would be utterly impossible. So, JIMO will do what Europa Orbiter was supposed to do, and much more. This is why the mission was chosen, to demonstrate the capability of space nuclear power.

Such nuclear reactors, which are much more powerful than the small no-moving parts radioisotope thermoelectric generators (RTGs) used on Voyager, Galileo and Cassini, have flown in Earth orbit before, on power-hungry radar surveillance satellites. However, they have never been used in deep space. Ion thrusters have been used on solar-powered earth satellites, on NASA's DS-1 spacecraft that visited a comet two years ago and currently on ESA's SMART-1 Moon probe, but the combination of nuclear power and ion propulsion (NEP - Nuclear Electric Propulsion) is new.

Power packed
The huge amounts of power available may even let us detect a simple signal from JIMO at Jupiter with a backyard satellite dish, as an education or hobbyist experiment. But more importantly, it will permit enormous data rates - sending back 10 megabits per second rather than the 100 kilobits per second typical for Voyager or Cassini.

Planetary scientists, so used to squeezing data out of instruments running with 50W or so, the power of a desk lamp, have been challenged with making the most of tens of kilowatts, the power of stadium floodlights. Obvious ideas are powerful radars to penetrate the icy shells of the satellites, to find how deep their liquid water oceans are buried. More radical ideas included using lasers, electromagnetic rail guns or the beam from the ion thrusters to blast material from the surface for analysis.

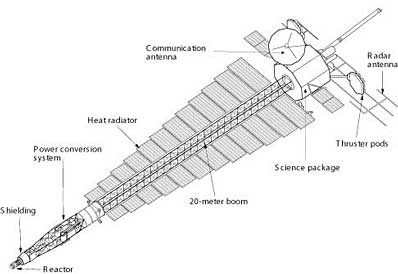
An illustration of Jupiter Icy Moons Orbiter. Credit: NASA/JPL

It is very early days for JIMO, which will not fly before 2011 at the earliest. But as currently envisioned, it will weigh perhaps 20 tonnes, and be perhaps 20 metres long. A large boom keeps the delicate scientific payload away from the reactor, which may develop around 100 kW of electrical power using a turbine driven by the reactor's heat. The heat has to be rejected by large radiator panels along the length of the vehicle.

It may take 6-8 years to spiral away from Earth and reach Jupiter, where it would spiral into orbit Callisto, then Ganymede, for about 8 months each, and then to Europa where it would operate for about 2.5 months. All in all, the mission may take 12 years.

There is a postscript to JIMO. It is intended as only the first of a series of missions - it makes little sense to invest several billion dollars in a one-off design. Where might the next Prometheus mission go? The bets are on Neptune, or Saturn's moon Titan to follow up on the Cassini mission.

Possible JIMO quests
Although the science mission has yet to be determined for this mission, Ralph Lorenz speculates for Astronomy Now on what scientific quests JIMO may embark.

Quest one: Finding Europa's weak spots
Planetary scientists are convinced there is an ocean on Europa, the only debate is how thick is the ice above it. Many think it may be between 8 and 20 km thick underneath Europa's few craters. Others, that there may be even thinner spots or cracks where the ice is thin. JIMO could investigate where the ocean is most accessible to aid the planning of future landing missions.

Quest two: The Jovian system as a dynamic environment
Does the ocean spray out like a geyser from cracks in Europa? Exactly how do Jupiter's storms produce lightning? How variable are Jupiter's aurora and the intense radiation belts close to Jupiter? Do Io's volcanoes, driven by tidal heating, erupt at regular intervals? A powerful camera would, if mounted on JIMO, be able to actually see the change in Io's shape due to the tides, all the way from Europa. The long duration of JIMO and its high data rate will make possible detailed, long-term monitoring of the dynamic Jovian system.

Quest three: What is everything made of?
Are there traces of organic molecules in Europa's ice, and how does the radiation alter them? How much water and ammonia is really on Jupiter - the Galileo probe only sampled one spot? What are the rings made of? Spectral maps from the ultraviolet to the far infrared could tackle these questions, together with in-situ measurement of the composition of dust and plasma - perhaps some of it to be created by lasers blasted at the satellite surfaces.

Quest four: The structure and evolution of the icy satellites
Do Callisto and Ganymede really have oceans, and how deep are they? Does Ganymede have a metal core? Important measurements to be taken are the gravity and magnetic fields of the satellites, together with precise measurement of their surface topography from laser altimeters or high-resolution radar imaging. One challenge is that the powerful electrical generator on JIMO may interfere with magnetic measurements. Gravity measurements are similarly difficult during thrusting.

Ralph Lorenz is a planetary scientist at the University of Arizona. His book, co-authored by Jacqueline Mitton, Lifting Titan's Veil is published by Cambridge University Press.